Рассмотрим примеры:

«Вы выходите на следующей остановке?» - спросил мальчик женщину в автобусе. «Нет» - ответила она. Сколько информации содержит ответ?  -  Согласно определению, ответ содержит один бит информации.

Или такой пример. Вы подошли к светофору на пешеходном переходе, когда горел красный свет. Загорелся зелёный. Здесь вы также получили один бит информации.

Итак, мы выяснили, когда сообщение несёт 1 бит информации.

Значит в примерах с кубиком и спортсменами количество информации будет больше. Давайте выясним как измерить это количество.

Рассмотрим пример. Занятия могут состояться в одном из кабинетов, номера которых от одного до шестнадцати. Ученики спросили у учителя: «в каком кабинете будут проходить занятия?» На что учитель им ответил: «Угадайте ответ за четыре вопроса, на которые я могу дать ответ «Да» или «Нет»».

Подумав староста класса задала следующие вопросы:

1 вопрос. Номер кабинета меньше 9? – Да. Ответил учитель

2 вопрос. Номер кабинета больше 4? – Да.

3 вопрос. Номер кабинета чётный? – Нет.

4 вопрос. Номер кабинета 5? – Нет.

Ученики поняли, что занятия состоятся в кабинете номер 7.

Итак, сколько же информации получили ученики?

Первоначально неопределённость знания (количество возможных кабинетов) была равна 16. С ответом на каждый вопрос неопределённость знания уменьшалась в два раза и, следовательно, согласно данному выше определению, передавался 1 бит информации.

Первоначально было 16 вариантов. После первого вопроса осталось 8 вариантов, и ученики получили 1 бит информации.

После 2 вопроса осталось 4 варианта, и ученики получили ещё 1 бит информации.

После 3 вопроса осталось 2 варианта и был получен ещё 1 бит информации.

И, наконец после 4 вопроса, остался 1 вариант и получен ещё 1 бит информации.

То есть мы можем сделать вывод, что ученики получили четыре бит информации.

Такой способ нахождения количества информации, называется методом половинного деления: здесь ответ на каждый заданный вопрос уменьшает неопределённость знания, которая имеется до ответа на этот вопрос, наполовину. Каждый такой ответ несёт 1 бит информации.

Нужно отметить, что методом половинного деления наиболее удобно решать подобные проблемы. Таким способом всегда можно угадать, например, любой из 32 вариантов максимум за 5 вопросов.

Если бы поиск совершался последовательным перебором: «Мы будем заниматься в первом кабинете?»  «Нет», «Во втором кабинете?»  «Нет» и т. д., то про седьмой кабинет можно было бы узнать после семи вопросов, а про восьмой — после восьми.

Теперь мы можем полученные результаты описать с помощью следующих определений:

•        сообщение об одном из двух равновероятных исходов некоторого события несёт 1 бит информации;

•        сообщение об одном из четырёх равновероятных исходов некоторого события несёт 2 бита информации;

•        сообщение об одном из восьми равновероятных исходов некоторого события несёт 3 бита информации.

Для того чтобы при измерении одной и той же информации получалось одно и то же значение количества информации, необходимо договориться об использовании определённого алфавита.

Пусть N – это количество возможных исходов события или неопределённость знания. Тогда i – это количество информации в сообщении об одном из N результатов.

Вернёмся к нашим примерам.

Обратите внимание, между данными величинами есть связь, которая выражается формулой.

Эта формула вам уже знакома. Также вы с ней встретитесь ещё не раз. Эта формула очень важна, поэтому её называют главной формулой информатики.

Для определения количества информации I, содержащейся в сообщении о том, что произошло одно из N равновероятных событий, нужно решить уравнение.

 

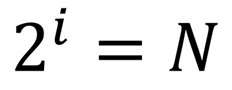
В математике такое уравнение называется показательным.

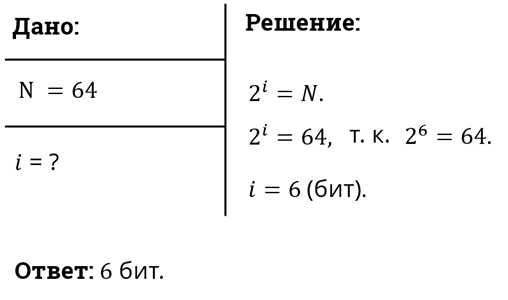
Рассмотрим пример. В коробке лежало 64 разноцветных катушки ниток. Сколько информации несёт сообщение о том, что из коробки достали жёлтую катушку?

Рассмотрим следующий пример.

В скором поезде Москва – Санкт-Петербург 8 вагонов, в каждом вагоне 32 места. Нужно определить какое количество информации несёт сообщение о том, что вам купили билет в 6 вагон, 13 место?

Этот пример показывает выполнение закона аддитивности количества информации (правило сложения): количество информации в сообщении одновременно о нескольких результатах независимых друг от друга событий равно сумме количеств информации о каждом событии отдельно.

Итак, мы уже говорили о том, что с формулой 2ⁱ = N мы уже встречались на прошлом уроке, когда говорили об алфавитном подходе к измерению информации. Тогда N рассматривалось как мощность алфавита, a i — как информационный вес каждого символа алфавита.

Если допустить, что все символы алфавита появляются в тексте с одинаковой частотой, то есть равновероятно, то информационный вес символа i идентичен количеству информации в сообщении о появлении любого символа в тексте. При этом N — неопределённость знания о том, какой именно символ алфавита должен стоять в данной позиции текста. Это замечание показывает связь между алфавитным и содержательным подходами к измерению информации.

Рассмотрим пример: Требуется угадать задуманное число из диапазона целых чисел, например, от 1 до 100. Чему равно количество информации в сообщении о том, что загаданное число 89?

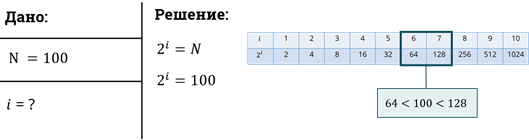
То есть, если значение N равно целой степени двойки, то показательное уравнение легко решить, а если нет, как в нашем примере. Как поступить в этом случае?

Можно догадаться, что решением уравнения будет дробное число, которое находится между 6 и 7.

В математике существует функция, с помощью которой решаются показательные уравнения. Эта функция называется логарифмом.

Тогда решение показательного уравнения запишется i равно логарифм N по основанию 2. Это означает, что мы должны найти степень, в которую нужно возвести основание, в нашем случае 2, чтобы получить N.

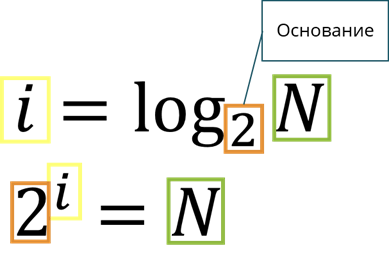
Например, для целых степеней двойки получим:

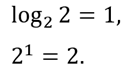
И так далее.

Значения логарифмов находятся с помощью специальных логарифмических таблиц. Также можно использовать инженерный калькулятор или табличный процессор.

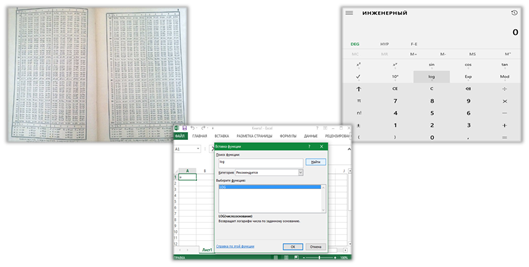
Определим количество информации, полученной из сообщения об угадывании задуманного числа из диапазона от одного до ста, с помощью электронной таблицы.

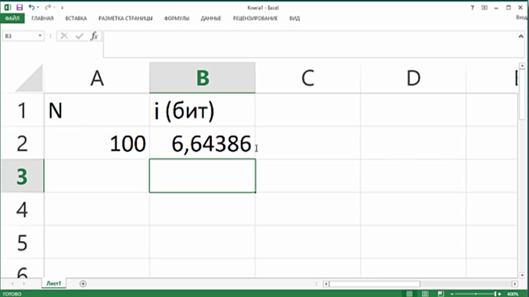
Количество информации в сообщении о том, что загаданное число 89 приблизительно равно 6,64 бит.

Формула для измерения количества информации была предложена американским учёным-электронщиком Ральфом Хартли, который является одним из основоположников теории информации.

Данный пример показал, что количество информации, определяемое с использованием содержательного подхода, может быть дробной величиной, если же находить информационный объем, путём применения алфавитного подхода, то там может быть только целочисленное значение.

Итоги урока.

В содержательном подходе количество информации, заключённое в сообщении, определяется объёмом знаний, который это сообщение несёт получающему его человеку.

Один бит - это минимальная единица измерения количества информации.

Сообщение, уменьшающее неопределённость знания в два раза, несёт один бит информации.

Для измерения количества информации применяется формула Хартли: