Универсальность дискретного представления информации . Содержательный подход.

Количество информации в одном том же сообщении, с точки зрения разных людей, может быть разным. Например, для человека, который не владеет английским языком, статья, напечатанная на английском языке, не несёт никакой информации. Информативным для человека является то сообщение, которое содержит новые и понятные сведения.

Давайте попробуем определить количество информации с позиции «информативно» или «неинформативно» для ученика 10 класса.

Столица России – Москва (это сообщение неинформативно, так как всем известно).

Высота Останкинской телебашни составляет 540 метров (или 45 этажей). Это делает её 6 по высоте конструкцией в мире (это сообщение информативно).

Корреляция, корреляционная зависимость — это зависимость между величинами, каждая из которых подвергается неконтролируемому разбросу (неинформативно, так как непонятно).

Необходимо отличать понятия информация и информативность.

Например, содержит ли учебник по информатике для десятого класса информацию? Конечно содержит, но для кого он будет информативным – для ученика десятого класса или первого класса? Естественно для ученика десятого класса. Первоклассник ничего из этого учебника не поймёт.

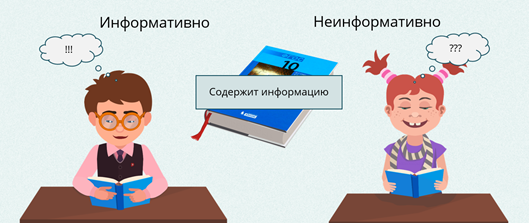
Теперь мы можем сделать вывод: количество информации зависит от информативности.

Информативность можно обозначить единицей, неинформативная информация равна нулю. Но это не даёт точного определения количества информации.

Алфавитный подход применяется для измерения информации, используемой компьютером. Так как компьютер не понимает смысла информации.

Содержательный подход применяется для измерения информации, используемой человеком.

В содержательном подходе, количество информации, заключённое в сообщении, определяется объёмом знаний, который это сообщение несёт получающему его человеку.

Вспомним, что с «человеческой» точки зрения информация - это сведения, которые мы получаем из внешнего мира.

Тогда сущность содержательного подхода заключается в следующем: количество информации, заключённое в сообщении, должно быть тем больше, чем больше оно пополняет наши знания.

То есть, чем больше первоначальная неопределённость знания, тем больше информации несёт сообщение, снимающее эту неопределённость.

Рассмотрим примеры.

Допустим, вы бросаете монету, загадывая, что выпадет: орёл или решка. Есть всего два возможных результата бросания монеты.

Причём ни один из этих результатов не имеет преимущества перед другим. В таком случае говорят, что они равновероятны.

В данном случае с монетой, перед её подбрасыванием неопределённость знания о результате равна 2.

Если же бросать игральный кубик с шестью гранями, то он может с равной вероятностью упасть на любую из них. Значит, неопределённость знания о результате бросания кубика равна 6.

Или такая ситуация: спортсмены-бегуны перед забегом путём жеребьёвки определяют свои порядковые номера на старте. Допустим, что в забеге участвует 100 спортсменов, тогда неопределённость знания спортсмена о своём номере до жеребьёвки равна 100.

Неопределённость знания о результате некоторого события - это количество возможных результатов исхода события.

Вернёмся к спортсменам-бегунам.

Здесь событие – это жеребьёвка спортсменов; исход – спортсмену выпал, например, номер 34.

Итак, в первом примере возможны два варианта ответа: орёл, решка; во втором примере шесть вариантов: 1, 2, 3, 4, 5, 6.

В третьем примере – 100 вариантов, может выпасть номер от 1 до 100.

Теперь, согласно определению, можно сделать вывод, что наибольшее количество информации несёт третье сообщение, так как неопределённость знания об исходе события в этом случае была наибольшей.

В 40-х годах 20 века Клод Шеннон — американский учёный и инженер, один из создателей математической теории информации, решил проблему измерения информации.

Шеннон дал такое определение информации: Информация – это снятая неопределённость знания человека об исходе какого-то события.

Вернёмся к примеру, с монетой. После того как вы бросили монету и посмотрели на неё, вы получили зрительное сообщение, что выпал, например, орёл. Определился один из двух возможных результатов. Неопределённость знания уменьшилась в два раза: было два варианта, остался один. Значит, узнав результат бросания монеты, вы получили 1 бит информации.

Сообщение об одном из двух равновероятных результатов некоторого события несёт 1 бит информации.

А также сообщение, уменьшающее неопределённость знания об исходе некоторого события в два раза, несёт 1 бит информации.